About

At present, the quest for higher critical current in superconductors is carried out via the Edisonian process of laborious experimental trial and error. It was found, for example, that pinning in copper oxide high-temperature superconductors can be enhanced by the addition of rare earth elements (Dy, Ho, etc.) to the materials fabrication mix. These additions generate insulating nanoparticle precipitates, which may self-assemble either into isolated nanoparticles or into arrays of columnar rods, substantially improving the current-carrying capacity of the material. However, there is no fundamental understanding of the mechanisms governing the pinning of large vortex arrays by a distribution of such defects, nor is there a satisfactory quantitative model predicting the critical current performance of a given pinning defect array. This conspicuous gap in our fundamental understanding is a major impediment to rapid progress in improving the performance of superconducting wires for applications. Here we propose to address this gap in collaboration with SciDAC Institutes using large-scale computation and leveraging DOE’s leadership-class computing facilities.

Vortices composed of supercurrents circulating around a normal core determine all the electrodynamic responses of superconductors to electric and magnetic fields. The dynamics of large scale arrays of vortices, which determine fundamental superconducting features such as the maximum lossless current, or critical current, remain poorly understood. The reason is the complexity of the vortex system, consisting of flexible vortex lines that interact with each other and with arrays of pinning defects in the composition and structure of the host superconductor; these pinning defects retard or fully halt the motion of vortices, the basic requirement for achieving current flow without energy loss. While the behavior of a single vortex interacting with a single pinning defect is fairly well understood, the transition to large numbers of vortices and pinning defects introduces new features that quickly become intractable, such as the mutual long-range repulsion among vortices and the many pinning configurations for the vortex array.

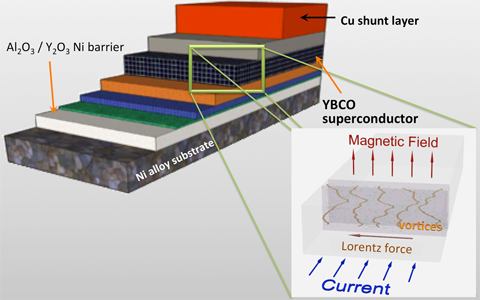Schematics of a second-generation superconducting wire: YBa₂Cu₃O₇ coated conductor, complex multilayer architecture of inexpensive materials. Inset shows the dynamics of vortices in the conductor in the presence of pinning centers.

In the transition to large numbers, much of the intuition developed for small numbers is lost. Carrying a lossless current, for example, requires all the vortices to be fully trapped by pinning defects; if significant numbers of vortices move, they dissipate energy and a finite resistance appears. We can calculate the pinning force of one columnar pinning defect on one vortex line and estimate the critical current a macroscopic array should support. Large arrays of vortices, however, attain only 20%-30% of the maximal theoretically possible critical current, which is given by the depairing current density. The origin of this “glass ceiling” for critical current is not known, but presumably it reflects low energy mechanisms for vortex motion in large arrays that do not occur in small arrays. It tells us that small-array theory and simulations are not good guides to large-array behavior.

The issues that emerge for large-scale arrays include the mutual long-range repulsion among vortex lines allowing the motion or trapping of a given line to influence many of its neighbors, the flexibility of vortex lines allowing them to simultaneously seek and attach to many pinning defects at different locations and to move in intricate dynamic configurations as vortex segments detach from one pinning defect and attach to another, the interruption of superconducting current pathways by non-superconducting pinning defects that reduce the cross-sectional area available for supercurrent flow, and the possibility of vortices cutting and reconnecting in new configurations during their motion. Although predicting the behavior of large-scale arrays of vortices is a fundamental challenge of high practical value, it has remained out of reach of analytical theory and conventional numerical simulation.

We propose to use the time-dependent Ginzburg-Landau (TDGL) formulation of vortex behavior to capture the dynamics of large-scale arrays of vortices. TDGL is a field formulation that does not require tracking the motion of each individual vortex line. Instead, the TDGL formalism treats the superconductor as a continuous field describing the superconducting medium, punctuated by an array of singularities representing the vortices that arise spontaneously in the presence of a magnetic field. An arbitrary array of pinning defects is distributed throughout the superconducting medium, which attracts vortices by lowering their free energy if their cores overlap the pinning defects. The attractive pining potential is widely tunable by adjusting the size and shape of the pinning defects. The TDGL equations automatically take into account the flexibility of vortex lines, long-range mutual vortex repulsion, vortex cutting and reconnecting, and the interruption of current paths by replacement of current carrying superconductor with insulating pinning defects. The challenge of this appealing TDGL formulation of vortex dynamics is the intense computational platform needed to represent a macroscopic array of vortices and pinning sites. Earlier TDGL formulations of vortex dynamics were restricted to modest sized systems where the full macroscopic behavior did not emerge.

Recent developments in DOE’s leadership-class computing hardware and scalable algorithms create a unique opportunity to bring the numerical exploration of superconductors to a new level. Using the leadership-class computing resources at Argonne, we will develop large-scale TDGL simulations that treat a fully macroscopic system of vortices and pinning defects. This formulation will allow systematic investigations of the effect on the critical current of temperature, magnetic field strength and orientation, and the size, shape and concentration of pinning defects. Our TDGL simulations have the advantage of high versatility. The simulations will be applicable not only to the copper oxide high-temperature superconductors, now the most promising for applications, but also to any other superconducting family by simply adjusting the materials dependent phenomenological parameters of superconducting coherence length, penetration depth, vortex elasticity and transition temperature. Our formulation will allow us to systematically answer the following questions: What is the maximum critical current that can be carried by a superconductor with a large array of vortices and pinning defects? What are the optimal size, shape, and concentration of pinning defects that achieve the maximum current? How do these parameters vary with temperature, the magnitude and the direction of the magnetic field, and the size of the system? Answering these questions in the context of a versatile TDGL simulation represents a major step forward for fundamental understanding the dynamics of macroscopic arrays of vortex lines and for practical development of high-critical-current superconductors for applications in the electricity grid.