Vortex dynamics in the magnetic field parallel to the current
Motivation
Recent experiments on Molybdenum-Germanium revealed an interesting and unexplained effect: If a magnetic field is applied in parallel with an external current, the superconductor shows a re-entrance behavior upon increasing the field. This means the magneto-resistance first increases with the magnetic field — as expected — but then decreases again at intermediate fields. This effect is strongly temperature dependent and can lead to a suppression of resistance below the measurable threshold over a range of a few kG. Here we are uncovering the underlying mechanism of the effect by large scale simulations. We study the vortex dynamics and magneto-resistance in this situation in the framework of a large-scale time-dependent Ginzburg Landau simulation. A small external current as well as the magnetic field are applied in the x-direction, the latter is then ramped up.
Results

Vortex configuration at intermediate fields, exhibiting a periodic dynamic resistive state, where vortex ends “travel” around the surface.
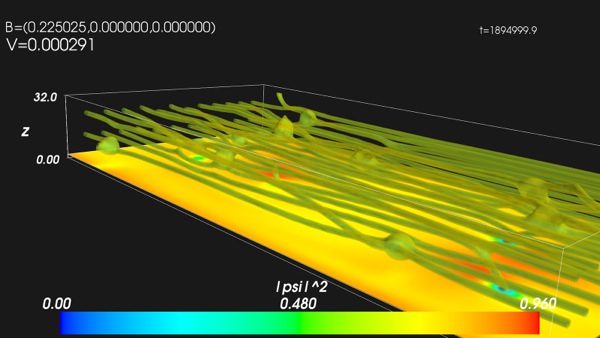
Vortex configuration at higher fields, where they straighten up and become “pinned” again.
Below are visualizations of a system of size 128×64×16 in units of the zero-temperature coherence length ξ0. The boundary conditions are periodic in x-direction and no-current boundaries in y- and z-direction. The number of grid points is 512×128×32. Simulations are for the infinite λ and neglecting fluctuations of the scalar potential. The current and field are applied in x-direction, where the current, Jx, is kept constant, while the magnetic field, Bx, is increased. The depairing current is: Jd ≈ 0.35 and Hc2(0) = 1 in our dimensionless units.
Jx = 0.3, 100 inclusions: current creates vortices, always resistive (avi).
Jx = 0.25, 100 inclusions: system becomes resistive at ∼ Hc1(Jx), no uncooked spaghetti state (avi).
Jx = 0.20, 100 inclusions: same as above with larger ∼ Hc1(Jx) (avi).
Jx = 0.10, no inclusions: fast ramp to uncooked spaghettis (avi).
Jx = 0.10, no inclusions: slow ramp to uncooked spaghettis (steady states), becomes resistive when current destabilized thermal fluctuations, no intermediate resistive state (avi).
Jx = 0.18, 2 inclusions: similar to the no inclusions case, without noticeable intermediate resistive state (avi).
Jx = 0.18, 10 inclusions: indication of intermediate resistive states, needs longer simulations to verify (avi).
Jx = 0.10, Bx = 0.05, no inclusions, different geometry: relaxation to single uncooked spaghetti (avi).
Jx = 0.18, Bx = 0.12, 10 inclusions: intermediate periodic dissipative state (avi).
